Производная

Определение. Производной функции 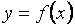 называется предел отношения приращения функции к приращению независимой переменной при стремлении последнего к нулю (если этот предел существует):

Нахождение производной называется дифференцированием функции. Геометрический смысл производной состоит в том, что производная есть угловой коэффициент касательной к кривой y=f(x) в данной точке х_o; физический смысл - в том, что производная от пути по времени есть мгновенная скорость движущейся точки при прямолинейном движении s = s(t) в момент t₀.

Правила дифференцирования (нахождения производных):

Алгоритм составления уравнения касательной к графику функции y=f(x)

 y = f(x_о) + f ′(x_о) (x – x_о) уравнение касательной

1. Вычислить f(x_о).

2. Вычислить  производные f ′(x) и f ′(x_о).

3. Внести найденные числа x_о,  f(x_о),  f ′(x_о) в уравнение касательной и решить его.

Пример: Найдем уравнение касательной к графику функции f(x) = x³ – 2x² + 1 в точке с абсциссой 2.

Решение.

Следуем алгоритму.

1) Точка касания x_о равна 2. Вычислим f(x_о):

 f(x_о) = f(2) = 2³ – 2 ∙ 2² + 1 = 8 – 8 + 1 = 1

2) Находим f ′(x). Для этого применяем формулы дифференцирования, изложенные в предыдущем разделе. Согласно этим формулам, х² = 2х, а х³ = 3х². Значит:

f ′(x) = 3х² – 2 ∙ 2х = 3х² – 4х.

Теперь, используя полученное значение f ′(x), вычислим f ′(x_о):

f ′(x_о) = f ′(2) = 3 ∙ 2² – 4 ∙ 2 = 12 – 8 = 4.

3) Итак, у нас есть все необходимые данные: x_о = 2, f(x_о) = 1, f ′(x_о) = 4. Подставляем эти числа в уравнение касательной и находим окончательное решение:

у = f(x_о) + f ′(x_о) (x – x_о) = 1 + 4 ∙ (х – 2) = 1 + 4х – 8 = –7 + 4х = 4х – 7.

Ответ: у = 4х – 7.

1. Алгоритм исследования непрерывной функции y=f(x) на монотонность и экстремумы

   1. Найти производную f `(x).
   2. Найти стационарные и критические точки.
   3. Отметить стационарные и критические точки на числовой прямой и определить знаки производной на получившихся промежутках.
   4. Опираясь на теоремы, сделать выводы о монотонности функции и о ее точках экстремума.
   
   
   Пример: Найти экстремумы функции f(x) = 2x³ - 15x²+ 36x - 14.

   Решение. Так как f ^'(x) = 6x² - 30x +36 = 6(x -2)(x - 3), то критические точки функции x₁ = 2 и x₂ = 3. Экстремумы могут быть только в этих точках. Так как при переходе через точку x₁ = 2 производная меняет знак плюс на минус, то в этой точке функция имеет максимум. При переходе через точку x₂ = 3 производная меняет знак минус на плюс, поэтому в точке x₂ = 3 у функции минимум. Вычислив значения функции в точках
   x₁ = 2 и x₂ = 3, найдем экстремумы функции: максимум f(2) = 14 и минимум f(3) = 13.

   2. Алгоритм отыскания наименьшего и наибольшего значений непрерывной
   функции y=f(x) на отрезке [a;b]

   1. Найти производную f `(x).
   2. Найти стационарные и критические точки функции, лежащие внутри отрезка [a;b].
   3. Вычислить значения функции y=f(x) в точках, отобранных на втором шаге, и в точках a и b; выбрать среди этих значений наименьшее (это будет yнаим.) и наибольшее (это будет yнаиб.)
   
   
   Пример 1. Найти наименьшее и наибольшее значения функции  на отрезке [-1, 2].

   Решение. Находим производную данной функции . Приравняем производную нулю () и получим две критические точки:  и . Для нахождения наименьшего и наибольшего значений функции на заданном отрезке достаточно вычислить её значения на концах отрезка и в точке , так как точка  не принадлежит отрезку [-1, 2]. Эти значения функции - следующие: 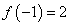,, 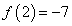. Ответ: наименьшее значение функции, равное -7, достигается на правом конце отрезка - в точке , а наибольшее, равно 9, - в критической точке .

1. Пример 2.  Найти наименьшее и наибольшее значения функции  на отрезке .
   Решение. Находим производную данной функции:
   
   Приравниваем производную нулю:
   
   Единственная критическая точку  принадлежит отрезку . Для нахождения наименьшего и наибольшего значений функции на заданном отрезке находим её значения на концах отрезка и в найденной критической точке:
   
   Ответ: функция достигает наименьшего значения, равного , в точке и наибольшего значения, равного , в точке .

Пример: Исследовать функцию и построить график:  y= 5x³ - 3x⁵.

Решение:

1) Область определения: D(y)= (-∞;+∞).

2) Найдем стационарные точки:

y'= 15x² - 15x⁴,

y'= 15x²(1 - x²)= 15x²(1 - x)(1 + x),

15x²(1 - x)(1 + x)= 0,

x= 0; ±1.

3) Определим вид стационарной точки и характер монотонности:

Точка x= -1 – точка минимума. 
Точка x= 0 – точка перегиба, функция в этой точки так же возрастает, но вогнутость меняется в другую сторону. 
Точка x= 1 – точка максимума.

Найдем значение функции в точке x= -1: y(-1)= 5(-1)³ - 3(-1)⁵= -2.
Найдем значение функции в точке x= 0: y(0)= 5(0)³ - 3(0)⁵= 0.
Найдем значение функции в точке x= 1: y(1)= 5(1)³ - 3 (1)⁵= 2

5) Исследуем функцию на четность: y(-x)= 5(-x³) - 3(-x⁵)= -5x³ + 3⁵= -y(x)
По определению функция нечетная, и график симметричен относительно начало координат.

Итак, функция нечетная.
Наша функция убывает на промежутке равном (-∞;-1).
x= -1 – точка минимума. Функция возрастает на (-1;1).
x= 0 – точка перегиба.
x= 1 – точка максимума. Функция возрастает на (1;+∞).